Lexikon
Gruppentheorie
eine mathemat. Theorie der modernen Algebra, die die Struktur von Gruppen untersucht. Eine Gruppe (3) erhält ihre besondere Struktur dadurch, dass zwischen ihren Elementen eine spezielle Operation definiert wird; Gruppen, die sich ihrer Struktur nach nicht unterscheiden, heißen zueinander isomorph. Die G. ermöglicht darüber hinaus eine Klassifikation von Gruppen nach verschiedenen Eigenschaften ihrer Struktur. Da die Elemente von Gruppen neben Zahlen auch Abbildungen (z. B. Kongruenz, Ähnlichkeit u. a.), Transformationen (z. B. Spiegelung, Drehung, Lorentztransformation) u. Symmetrien sein können, spielt die G. in der Geometrie u. auch in der Physik eine wichtige Rolle: Sie ermöglicht eine Klassifikation von solchen Objekten, die gegenüber diesen Abbildungen, Transformationen oder Symmetrien invariant sind. Auf diese Weise gelang erstmals Felix Klein eine Klassifikation der verschiedenen Geometrien.
In der Physik führt die Untersuchung der Gruppe der Lorentztransformationen zu einer Klassifikation der Physik in relativistische u. nichtrelativistische Physik. Durch die Untersuchung der Eigenschaften von Symmetriegruppen lässt sich in der Kristallographie ein Überblick über alle möglichen Kristallformen geben.
L. Baumgartner, G. 51972. – H. Siemon, Anwendungen der elementaren G. 1981.

Wissenschaft
Kosmischer Babyboom
Vor etwa zehn Milliarden Jahren entstanden auf einen Schlag sehr viele Sterne. Seither sinkt die Geburtenrate – und inzwischen hat eine Art kosmischer Dämmerzustand begonnen. von THOMAS BÜHRKE Das Sternbild Fornax (Chemischer Ofen) besteht nur aus wenigen lichtschwachen Sternen. Doch Kosmologen fanden dort den sprichwörtlichen...
Wissenschaft
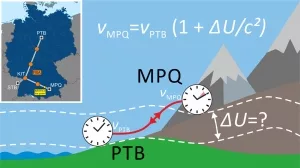
Relativistisch genau – Atomuhren messen Höhenunterschiede
Albert Einstein sagte voraus, dass die Zeit auf Bergen oder sonstigen Erhebungen schneller vergeht als im Tal – schuld sind die höhenbedingten Unterschiede in der Erdschwerkraft. Jetzt ist es Physikern gelungen, den winzigen Effekt der gravitativen Zeitdehnung für die Höhenmessung selbst weit voneinander entfernter Orte zu nutzen...

