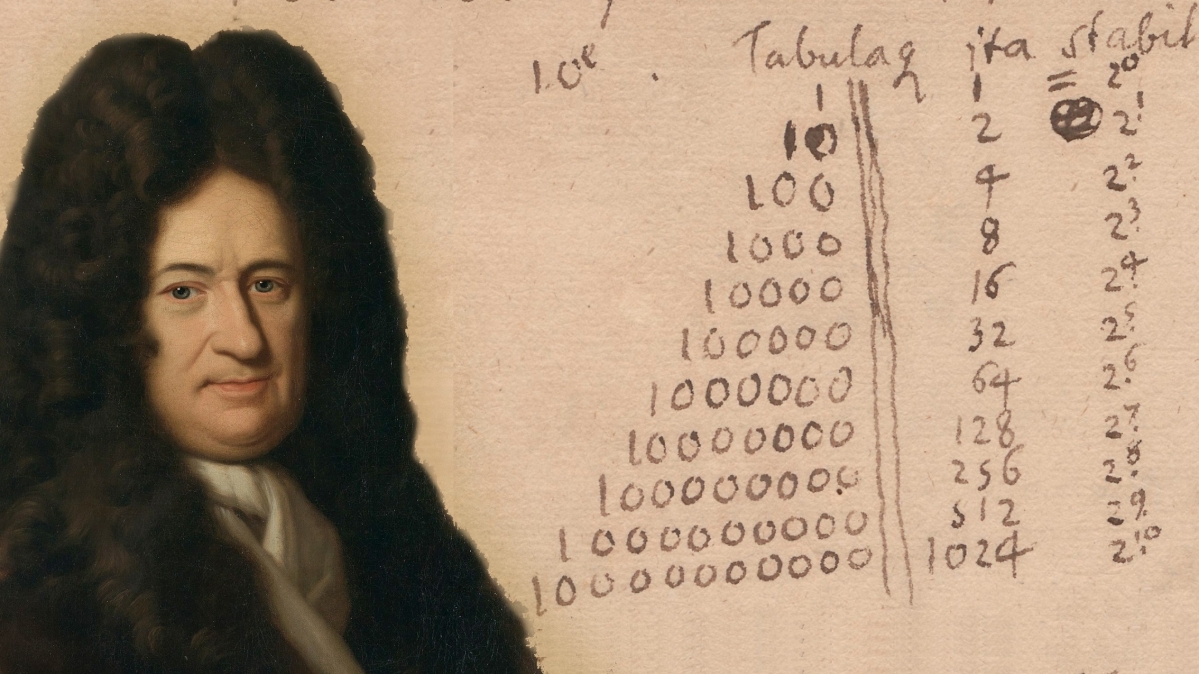wissen.de Artikel
Leibniz - Universalgelehrter und Mathegenie
Leibniz wurde 1646 in Leipzig geboren und erwies sich schon früh als ziemlich schlaues Kerlchen. So brachte er sich zum Beispiel bereits mit sieben Jahren selbst Latein bei, fing mit 15 Jahren an zu studieren und promovierte schon mit 22. Das wäre heute schon eine beachtliche Leistung, für die damaligen Verhältnisse war es das umso mehr.
Über die Jahre entwickelte sich Leibniz schließlich zu einem wahren Universalgenie und forschte auf vielen, ganz verschiedenen Fachgebieten. Eine besondere Leidenschaft hegte er jedoch für die faszinierende Welt der Zahlen. Er war überzeugt, alles in der Welt könnte mit ihnen berechnet und erklärt werden, wenn man nur die dahinterstehenden mathematischen Prinzipien entschlüsselt. Im Rahmen seiner Forschungen entwickelte Leibniz bis heute wichtige Grundlagen wie die Infinitesimalrechnung, die man noch heute in der Schule lernt, aber auch die mathematische Voraussetzungen für den Computer in Form des binären Zahlensystems.
Warum 111 das Gleiche sein kann wie sieben
Anders als unser "normales" Dezimalsystem, das wir im Alltag nutzen und das alle Zahlen mit den Ziffern von Null bis Neun darstellt, besteht das von Leibniz entwickelte, binäre Zahlensystem nur aus zwei Ziffern: Der Null, für Leibniz das Nichts, und der Eins, die für Leibniz als Symbol des Göttlichen stand. Binäre Zahlen wie 11001, 100101, 001110 setzen sich also allein aus den zwei Ziffern Null und Eins zusammen.
Auch wenn die Notation binärer Zahlen also auf diese zwei Ziffern begrenzt ist, können sie doch jeder beliebigen Zahl unseres Dezimalsystems entsprechen. Denn der Wert der einzelnen Ziffer hängt nicht von ihrer "Art" ab, so wie wir es von einer fünf oder drei gewöhnt sind, sondern von ihrer Position in der binären Zahl. Das kann man sehr gut erkennen, wenn man binäre Zahlen in unser Dezimalsystem umwandeln möchte. Dann werden die einzelnen Ziffern, abhängig davon an welcher Stelle der binären Zahl sie stehen, mit verschiedenen Potenzen der Zahl Zwei multipliziert. So kann sich für die gleiche Ziffer jeweils ein ganz anderer Wert ergeben.
Ein Beispiel wäre die binäre Zahl 111. Bei einer Umwandlung in das Dezimalsystem wird aus dieser: 111= 1x20 + 1x21 + 1x22 = 1 + 2 + 4. Die Zahlen Eins, Zwei und Vier entsprechen also jeweils den Einsen aus der binären Zahl. Sie unterscheiden sich aber im Wert je nachdem, ob die Eins an der ersten, zweiten oder letzten Stelle der binären Zahl steht. Den Gesamtwert der binären Zahl erhält man dann, wenn man diese einzelnen Werte addiert: 1 + 2 + 4 = 7, entsprechend 7x100, denn auch das Dezimalsystem funktioniert nach diesem Schema.
Dadurch, dass also die 111 in unserem Zahlensystem der Sieben entspricht, sah Leibniz übrigens sein binäres Zahlensystem auch in religiöser Hinsicht bestätigt. Denn Gott hat laut biblischer Überlieferung die Erde in sieben Tagen geschaffen und in der 111 erkannte Leibniz passenderweise die Dreifaltigkeit Gottes.

Kein Computer ohne binäre Zahlen
Dieses binäre System ermöglicht es heute, dass Computer funktionieren, das heißt mathematische und logische Rechenoperationen durchführen sowie Informationen darstellen, versenden und empfangen können. Die Rechnungen dafür finden im Prozessor statt und werden hier erst durch die binären Zahlen überhaupt möglich. Denn die beiden Zustände Eins und Null kann der Computer durch Strom an und aus wiedergeben. In den mathematischen Rechenoperationen kann der Prozessor so mit den binären Zahlen addieren, subtrahieren, multiplizieren und dividieren.
Der binäre Code ist aber auch wichtig, um Informationen darzustellen. Woher weiß der Computer, was er uns zeigen muss, wenn wir auf eine bestimmte Taste drücken? Dazu müssen wir ihm sozusagen „unsere Welt“ beibringen, indem wir sie für den Prozessor in binäre Zahlen übersetzen. Mit diesen binären Codes kann letztlich alles uns Bekannte nur mit Einsen und Nullen dargestellt werden. So steht in dem ASCII Binärcode, mit dem Sonderzeichen und Buchstaben dargestellt werden können, die Zahlenfolge 0100 0001 für den Buchstaben "A" und genauso können auch Bilder, Ton und vieles mehr codiert werden.
Urahn des Computers
Aber Leibniz hat sich mit Zahlen und Mathematik nicht nur theoretisch beschäftigt, sondern auch gerne praktisch gearbeitet. So erfand er die erste Rechenmaschine, die alle vier Grundrechenarten beherrschte und die zu den Vorläufern der heutigen Computer zählt. Diese mechanische Rechenmaschine arbeitet schon damals nach dem sogenannten "EVA-Prinzip", also die vorgebene Trennung von Eingabe, Verarbeitung und Ausgabe von Daten, nach dem auch heutige Computer arbeiten.
Als Eingabe werden die Ausgangszahlen eingestellt, dann in der Verarbeitung durch Zahnräder im Inneren die Rechnung durchgeführt und danach die Lösung ausgegeben. Das Herzstück ist dabei eine kleine, verschiebbare Walze mit neun unterschiedlich langen Zähnen. Sie greift in ein Zahnrad und kann je nach Position verschiedene Zahlen repräsentieren. Um mit Leibniz' Rechenmaschine beispielsweise eine Zahl mit zwölf zu multiplizieren, muss man erst die Zahl einstellen, dann eine andere Kurbel zwei Mal für die Einerstelle der zwölf drehen und anschließend eine weitere Kurbel einmal für die Zehnerstelle. Durch weiteres Drehen wird dann diese Zahl zwölf Mal addiert, also mit zwölf multipliziert.
Auch wenn dieses Gerät noch mit Zahnrädern und Walzen statt mit Transistoren und Strom arbeitete, steckten in der Funktionsweise von Leibniz' Rechenmaschine schon einige Prinzipien, die sich auch in modernen Computern wiederfinden. Wenn wir heute unser Handy oder einen Rechner nutzen, profitieren wir damit immer auch ein wenig von den Vorarbeiten eines vor mehr als 250 Jahren geborenen Universalgelehrten.