Lexikon
Zahlen
ein auf der Tätigkeit des Zählens beruhender Begriff; Zahlen sind Glieder einer durch Zählen entstandenen Folge, die dadurch gekennzeichnet ist, dass jedes Glied einen bestimmten Platz hat, d. h., dass ihm ein wohlbestimmtes Glied vorangeht oder folgt. Werden Dinge gezählt, so ist das letzte Glied die Anzahl der Dinge. Die so entstandenen Zahlen heißen benannte Zahlen (4 Hunde, 6 Liter). Im Gegensatz dazu stehen die unbenannten Zahlen 1, 2, ..., auch Grundzahlen, natürliche Zahlen oder Kardinalzahlen genannt. Gerade Zahlen sind 2, 4, 6, ..., ungerade Zahlen 1, 3, 5, ... Die Zahlen als Platznummern in einer Reihe heißen Ordnungszahlen oder Ordinalzahlen (der Erste, Zweite, ...).
Die Grundrechnungsarten haben zu Erweiterungen des Zahlenbegriffs geführt. Durch die Subtraktion als Umkehrung der Addition gelangte man zu der Null und den negativen Zahlen, durch die Division als Umkehrung der Multiplikation zu den gebrochenen Zahlen (Brüchen). Die natürlichen Zahlen heißen im Gegensatz zu den negativen Zahlen und den Brüchen positive ganze Zahlen. Die gebrochenen Zahlen sind Quotienten zweier ganzer Zahlen. Sie werden mit Hilfe eines Bruchstrichs geschrieben; Bruch. Die ganzen und gebrochenen Zahlen heißen rationale Zahlen. – Eine besondere Art von Brüchen sind die Zehner- oder Dezimalbrüche, die auch als Dezimalzahlen geschrieben werden (3/10 = 0,3). Brüche, deren Nenner nicht Zahlen sind, die sich als Produkt von Potenzen der Zahlen 2 und 5 darstellen lassen, kann man in der Form von periodischen (unendlichen) Dezimalzahlen schreiben, z. B. 7/11 = 0,636363...
Durch die Umkehrungen von Potenzrechnung gelangt man zu den irrationalen Zahlen. Solche Zahlen sind z. B.
√2
= 1,4142 ... und lg 2 = 0,30103 ... (Wurzel; Logarithmen). Die irrationalen Zahlen werden eingeteilt in algebraische und transzendente Zahlen. Eine algebraische Zahl ist jede Zahl, die sich als Lösung einer algebraischen Gleichung ergibt; das sind alle aus Wurzelausdrücken zusammensetzbaren Zahlen, z. B. √2
+ √3
. Alle nicht algebraischen Zahlen heißen transzendente Zahlen, z. B. π, e, die Logarithmen, die meisten Werte der Winkelfunktionen. – Stellt man die rationalen Zahlen auf einer Geraden dar, so erfüllen sie die Gerade nicht restlos; zwischen ihnen liegen die irrationalen Zahlen. Z. B. liegt das Bild der Zahl √2
zwischen den Bildern der Zahlen 1 und 2 und (wenn man das Intervall verkürzt) weiter zwischen den Zahlen 1,4 und 1,5; 1,41 und 1,42; 1,414 und 1,415; 1,4142 und 1,4143 usw. Es lässt sich jedoch keine rationale Zahl angeben, deren Wert √2
genau ist, aber √2
kann durch eine Intervallschachtelung bestimmt werden. Die irrationalen Zahlen lassen sich auch durch unendliche nichtperiodische Dezimalzahlen beliebig genau angeben. Die bisher genannten Zahlen, d. h. rationale und irrationale Zahlen, bilden zusammen die reellen Zahlen.Bei der Lösung von quadratischen Gleichungen können sich imaginäre Zahlen ergeben, denn keine der bisher genannten Zahlen hat die Eigenschaft, dass die Quadratzahl negativ ist; aus x2 = – 1 folgt z. B.  dafür wurde das Zeichen i eingeführt. i heißt imaginäre Einheit. Die Zahlen a·i, wobei a eine der bisher betrachteten Zahlen ist, die im Gegensatz zu diesen Zahlen reelle Zahlen heißen, werden imaginäre Zahlen, die Zahlen der Form a + bi komplexe Zahlen genannt. 2 Zahlen der Form a ± bi heißen konjugiert komplexe Zahlen. Ebenso wie sich die reellen Zahlen als Vektoren längs einer Zahlengeraden darstellen lassen, stellt man die komplexen Zahlen in einer Ebene (Gauß’sche Zahlenebene) als Vektoren oder Zeiger dar.
dafür wurde das Zeichen i eingeführt. i heißt imaginäre Einheit. Die Zahlen a·i, wobei a eine der bisher betrachteten Zahlen ist, die im Gegensatz zu diesen Zahlen reelle Zahlen heißen, werden imaginäre Zahlen, die Zahlen der Form a + bi komplexe Zahlen genannt. 2 Zahlen der Form a ± bi heißen konjugiert komplexe Zahlen. Ebenso wie sich die reellen Zahlen als Vektoren längs einer Zahlengeraden darstellen lassen, stellt man die komplexen Zahlen in einer Ebene (Gauß’sche Zahlenebene) als Vektoren oder Zeiger dar.

Wissenschaft
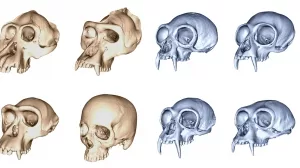
Der menschliche Schädel entwickelte sich schnell
Großes Gehirn, flaches Gesicht: Diese Merkmale kennzeichnen den menschlichen Schädel und unterscheiden ihn von den Schädelformen unserer nächsten Verwandten, den Menschenaffen. Eine Studie zeigt nun, dass sich der menschliche Schädel im Laufe der Evolution schneller entwickelt hat als bei allen anderen großen und kleinen...

Wissenschaft
Wirklich wahr?
Die Frage nach der Wahrheit ist ein Klassiker der Wissenschaftsphilosophie, und gerade in dieser Zeit besonders wichtig. von TOBIAS HÜRTER Es gibt eine merkwürdige Stelle in der Bibel, die man leicht überliest. Als Jesus im Amtssitz des römischen Statthalters Pontius Pilatus verhört wird und beteuert, er sei gekommen, um „für die...
Mehr Artikel zu diesem Thema
Weitere Artikel aus dem Kalender
Weitere Lexikon Artikel
Weitere Artikel aus dem Wahrig Fremdwörterlexikon
Weitere Artikel auf wissenschaft.de
Ultraharte Weichtier-Zähne
Das große Sterben
Quanten-Diamanten
News der Woche 28.11.2025
Das Nordmeer auf der Nachbarwelt
Walgesänge ähneln menschlicher Sprache

