wissen.de Artikel
Der Goldene Schnitt – das mathematische Geheimnis der Schönheit
Der Goldene Schnitt bezeichnet grundlegend ein bestimmtes Teilungsverhältnis in der Geometrie. Damit ist gemeint, dass zum Beispiel eine Strecke oder eine andere Größe auf eine bestimmte Art in zwei Teile geteilt wird. Diese Einteilung hat einen mathematischen Hintergrund und wirkt auf uns sehr ausgeglichen und harmonisch.
Die Goldene Zahl
Konkret wird eine Strecke für den Goldenen Schnitt in ein kürzeres und ein längeres Stück aufgeteilt. Dabei muss so eingeteilt werden, dass die Gesamtstrecke geteilt durch die längere Strecke das Gleiche ergibt wie die längere Strecke geteilt durch die kürzere Strecke – nämlich gerundet 1,618. Diese sogenannte Goldene Zahl, in der Mathematik als „Phi“ bezeichnet, ist dabei eine irrationale Zahl. Das heißt sie besitzt unendlich viele Nachkommastellen und lässt sich daher niemals vollständig errechnen und darstellen. Man kann sich ihr aber immer weiter annähern.
Dies gelang dem Mathematiker Leonardo Fibonacci, der im Jahr 1212 eine Zahlenfolge entwickelte mit der man sich erstmals der Goldenen Zahl auf immer mehr Nachkommastellen annähern konnte. In der später nach ihm benannten Fibonacci-Folge werden immer zwei aufeinanderfolgende Zahlen addiert. Diese beiden ergeben dann die nächste Zahl, die wieder mit der Zahl davor addiert wird: 1,1,2,3,5,8,13…55, 89, 144 und so weiter. Wenn man die aufeinanderfolgenden Zahlen durcheinander teilt, nähert man sich immer mehr der goldenen Zahl an. So ist 13 geteilt durch 8 noch gleich 1,625 und 144 geteilt durch 89 schon 1,618. Je höher die Zahlen in der Folge werden, desto genauer errechnet man die goldene Zahl 1,61803398...

Goldene Anfänge
Das mathematische Prinzip hinter dem Goldenen Schnitt wurde aber bereits lange vorher in der Antike durch den Mathematiker Euklid entdeckt. Er beschäftigte sich etwa um 300 vor Christus viel mit Geometrie und konstruierte mit Zirkel und Lineal eine Strecke mit dem genauen Teilungsverhältnis des goldenen Schnitts. Er beschrieb diesen auch erstmals in seinen Büchern der „Elemente“ und bezeichnete das Vorgehen als „Teilung einer Strecke nach dem äußeren und mittleren Verhältnis“
Der Begriff des Goldenen Schnitts wurde allerdings erst wesentlich später, im 19. Jahrhundert, von dem deutschen Mathematiker Martin Ohm geprägt und entwickelte sich aus der „göttlichen Proportion“, wie das Verhältnis seit Beginn des 16. Jahrhunderts genannt wurde. Verwendet wurde der Goldene Schnitt aber wohl schon lange vor Beginn der Mathematik und der Kenntnis von Zahlen. Viele Faustkeile der Steinzeit, mehrere zehntausend Jahre alte Werkzeuge unserer Vorfahren, wurden schon damals nach Proportionen gefertigt, die etwa Goldenem Schnitt entsprechen.
Schönheit in Kunst und Architektur
Das besondere Verhältnis des Goldenen Schnitts zieht sich seit der der Frühzeit der menschlichen Kultur durch die Kunst- und Architekturgeschichte. Wahrscheinlich, weil die meisten Menschen dieses goldene Teilungsverhältnis automatisch als sehr harmonisch empfinden. Es entstehen Verhältnisse und Proportionen, die für das menschliche Auge schön und ästhetisch wirken. So orientieren sich viele Gemälde, Statuen und Bauwerke an „goldenen Proportionen“.
Weltberühmte Beispiele sind dabei zum Beispiel die „Mona Lisa“ des Malers und Mathematikers Leonardo Da Vinci oder die Statue der „Venus von Milo“, deren Proportionen sich an dem goldenen Teilungsverhältnis orientieren. Aber auch in anderen bekannten Gemälden lässt sich dieses Verhältnis finden. So kann beispielsweise „Das Abendmahl“, ein Gemälde von Da Vinci, anhand der dargestellten Figuren nach dem Goldenen Schnitt in einen größeren und einen kleineren Teil eingeteilt werden, genau wie in Michelangelos Wandgemälde „Die Erschaffung Adams“, wo die Größen der Figuren im goldenen Verhältnis zueinanderstehen.
Was wir heute nicht wissen ist, inwiefern die Künstler damals tatsächlich auf den Goldenen Schnitt geachtet haben oder ihn durch ein natürliches Gefühl für die Harmonie von Proportionen eher unbewusst eigensetzt haben. Was allerdings gezeigt wurde, ist, dass manche Menschen dieses Gefühl bereits zur Eiszeit besessen haben. Etwa 15.000 Jahre alte Funde zeigen in Stein geritzte Figuren, deren Proportionen dem Goldenen Schnitt entsprechen.
Der Goldene Schnitt lässt sich aber genauso in der Architektur wiederfinden. Berühmte Beispiele sind Bauwerke wie der antike Pantheon Tempel in Griechenland oder die Cheops-Pyramide in Ägypten, in deren Maßen der Goldene Schnitt wiederzufinden ist. Auch Notre Dame, der Kölner Dom, das Leipziger Rathaus und viele weitere Bauwerke wurden nach diesem Verhältnis konstruiert.
Goldener Schnitt selbst bei unserem Körper
Der Goldene Schnitt ist aber keineswegs die „Erfindung“ des Menschen. Ursprünglich kommt er aus Natur und ist faszinierenderweise überall in der Welt um uns herum zu finden, sogar in uns selbst. Die Höhe unseres Bauchnabels teilt unseren Körper etwa in diesem Verhältnis und auch das Verhältnis unserer Nase zur Mundbreite ist „golden“.
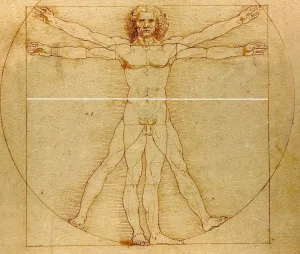
Ein bekanntes Beispiel für den goldenen Schnitt in unseren Proportionen ist Da Vincis sogenannter vitruvianischer Mensch, der mit ausgestreckten Armen und Beinen entweder in ein Quadrat oder einen Kreis passt. Hier lassen sich die göttlichen Proportionen überall wiederfinden, sowohl im dargestellten Menschen selber, als auch in dem Verhältnis von Kreis und Quadrat.

…und auch in der Natur
In verschiedenen Formen ist der Goldene Schnitt zudem auch immer wieder im Tier- und Pflanzenreich zu entdecken. So wachsen zum Beispiel die Blütenblätter von Rosen und anderen Pflanzen im goldenen Winkel. Das bedeutet, dass zwei aufeinanderfolgende Blätter in dem Winkel zueinanderstehen, der entsteht, wenn man einen Kreisumfang im goldenen Verhältnis teilt. Für die Pflanzen ist dies allerdings keine Frage der Ästhetik, sondern hilft ihnen dabei, optimal viel Sonnenlicht und Wasser aufzunehmen.
Häufig ist auch die sogenannte Goldene Spirale zu finden. Um diese darzustellen, wird ein Rechteck nach dem goldenen Schnitt geteilt, sodass ein neues Rechteck und ein Quadrat entstehen. Wiederholt man dies mehrfach, entstehen mehrere ineinander verschachtelten Quadrate, deren Seitenlänge sich jeweils aus der Summe der Seitenlängen der beiden nächsten, kleineren Quadrate ergibt. Ihre Größe basiert also auf der Fibonacci-Folge. Verbindet man nun die Ecken der Quadrate mit einer gebogenen Linie, entsteht die Goldene Spirale oder auch Fibonacci Spirale. Diese lässt sich beispielsweise in der Form von Muscheln, Farnen, Wirbelstürmen, sogar der Ananas und vielen weiteren Naturbeispielen erkennen.
